Understanding the InfiniBox Data Path
Want to understand the InfiniBox Data Path? Learn about it from Brian Carmody, INFINIDAT’s CTO. Transcript below:
[Brian Carmody, CTO, INFINIDAT] So continuing the actual data path discussion, right now what we kind of built out is we have this system for collecting data and kind of just putting it into the cache. So now we need to eventually start bringing media and destaging and everything into this process. So running on each of the views is a process called an allocator thread.
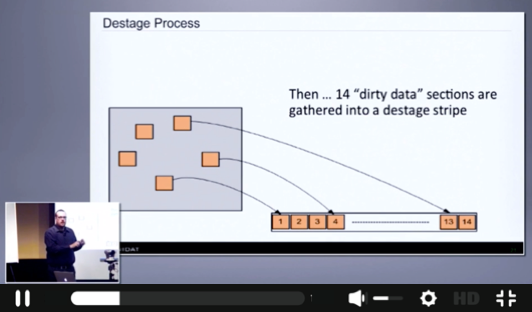
The job of the allocator is to pick data sections out of cache and to group them into structures that we call destage stripes. And each destage stripe has 14 data sections. It's in each of those sections is 64k of data and 4k of metadata.
So with that in mind, if we go back to that VDA, that linear space, that's the first of level virtualization down. You can think of it as just the concatenation of all of the stripes. And the trie of course, is the data structure that holds that mapping between the two.
So let me give you a little bit more detail about how that destage stripe and all that works. Along with picking 14 data sections out of memory, the allocator thread also computes parity. And we use a very simple parity mechanism. It is computed only with XORs. It runs on the general purpose CPU. There's no special hardware or anything like that.
There is no Reed-Solomon coding. In fact, our algorithm provably uses half the number of CPU cycles of any Reed-Solomon family code. So we take the message, we compute horizontal and diagonal parity, which becomes what we call P1 and P2. So on disk with protection, a stripe is actually 16. It's 14 data sections and two parity sections. Each of them is 64k data plus four at 68k. So the total is each stripe is 1.088 megabytes.
[Audience Member] Would a stripe like that come from multiple servers or only from one server?
[Brian Carmody] Multiple servers.
[Audience Member] So it would come multiple servers.
[Brian Carmody] Yeah. That's an excellent question. And I actually have two slides down to talk about how we --
[Audience Member] Perfect.
[Brian Carmody] -- Because I glossed over it, I said, it just chooses. There's actually a lot of computation that goes into the choosing. But to keep it simple, just to keep the display the discussion going, after the allocator computes parity and we have that array of 16 sections, the final thing it does is it assigns the stripe to a RAID group. RAID groups are invisible. Customers cannot see them or users cannot see them, and they are quite simply a bucket that stores stripes.
So think of this as a RAID group here. It has a width of 16 sections, and then it has a depth, which is based on whatever the size of the drives are. Each of the columns, each of the 16 columns we call a member or a column. Each of these members or each of these columns lives on exactly one partition of exactly one hard drive on the back end of the system.
To put it another way, each of these rectangles is one of the eight disk enclosures. Each of these cylinders is one of the 60 disk drives in the enclosure. On each disk drive is a number of partitions. Well, it's 246 if you're curious. Each of these the DPs are partitions, corresponds to exactly one column on a RAID group somewhere.
What we've done with this is we have created a very simple system that allows us to interleave lots of data from lots of different RAID groups onto an overlay or map it to a finite number of disk drives. And this is the secret to being able to do very fast rebuilds and have even performance, regardless of what the IO pattern is.
One thing I'll point out is we use what we call a minimum contention algorithm for assigning columns to partitions. It's static. It only changes when the topology of the array changes, when disk drives are edited or removed. And the way the algorithm works is it does two things.
Number one, it tries to keep the columns of a given RAID group as far away from each other on the back end as possible. So certainly not on the same disk drive. You don't want them bunching up on one disk enclosure. So you want two columns on each of eight disk enclosures.
But the algorithm also works to minimize the number of any two RAID groups that have common members on a disk drive. And the reason we do this is those unions are in the event of a triple disk failure or where the data loss will occur. So by keeping that as small as possible, it allows us to exit and get from n plus 2 to n plus 1 redundancy very, very quickly in the event of a single disk failure. And exiting that phase is critical for being able to have long-term resiliency.